Tony Finch – blog

Nico has a box of dominoes, and playing with it often consists of me trying to arrange them into nice patterns, and him trying to shuffle them. The box contains the usual 28 dominoes, but has coloured Paddington Bear pictures instead of spots. The dominoes can fit into the box in four stacks of seven; in this arrangement there are eight squares visible but the dominoes only have seven different pictures. There isn't a particularly satisfying choice of which four dominoes get to show their faces.

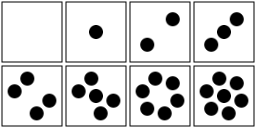
Traditional dominoes use the same six arrangements of spots as dice, plus blank. They are based on a 3x3 grid, in which the middle spot is present in odd numbers and absent in even numbers, and opposing pairs of spots are added starting with the diagonals. This extends nicely from zero to nine:

I could solve my four-pile problem with a set of 36 dominoes with faces numbered 1 to 8 (which I think is prettier than 0 to 7), or I could make five piles showing squares numbered 0 to 9 if I had a "double-nine" set of 55 dominoes.

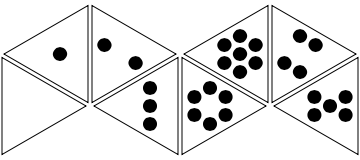
Another way to arrange the spots is hexagonally, which also allows you to use a translation from binary to unary. The middle dot represents bit 2^0; two opposing dots represent bit 2^1; and the other four dots in the hexagon represent bit 2^2:

I think this is even more pretty :-) It can also make nice octahedral dice, and the hexagon patterns will fit in the faces particularly well if the corners are rounded off.

ETA: Following the discussion in the comments, I have come up with an extended layout that works up to 31 spots. It fits fairly well in a square, but loses some of the hexagonal symmetry. It is based on the observation that three overlapping hexagonal rings contain 16 spots (3 * 6 - 2 overlapping spots). No great insight that shows how to extend it further, I am afraid. See dice-spot.html which includes the code to draw the diagrams.